How to Think About Planned Lead Times
By STEPHEN C. GRAVES
A fundamental construct of most planning systems, such as MRP (Material Requirements Planning) and DRP (Distribution Requirements Planning), is the notion of a planned lead time. Associated with each production activity or stage is a lead time that forms the basis for production and transportation planning, and material procurement. These lead times, along with inventory targets, are the primary control mechanisms for deciding when to order raw materials, when to initiate production or transportation activities, and when to schedule final assemblies in order to satisfy a given set of demand requirements.
There is extensive literature and models for guiding the setting of inventory targets (e.g., the reorder points and safety stock levels). Yet there is very limited guidance from practice or theory on how to set planned lead times. In my experience, the planned lead times are set based on experience and observation; if the actual lead time for a production activity often exceeds the planned lead time, then we need to increase the planned lead time. Furthermore, extreme events have an undue impact: if we had a delivery failure, then a common response is to increase the lead times for production so that it doesn’t happen again.
But is this the best way to manage and set these parameters? The intent of this note is to provide a brief, critical examination of planned lead times: why are they used and why are they important? What should be considered in setting these control variables and what are the trade-offs? And how might a simple model help to highlight the key factors that drive the planned lead times.
Why do most formal and informal planning systems rely on planned lead times?
The short answer is that we don’t have a better solution. Planned lead times are a very effective mechanism for decomposing a complex planning problem in a way that matches organizational realities; that is, they simplify a hard problem.
Consider a simple example: suppose you manufacture customized mechanical kitchen timers. You acquire the mechanism from your machine shop with a relatively long lead time; and you acquire the housing from your injection molding operations with a shorter lead time. You assemble a standard “vanilla” timer in-house, where assembly combines the mechanism into the housing, along with other hardware components. Upon receipt of an order, you then customize the timers according to the customer’s specifications, e.g., labeling and packaging. In order to provide customer service, you make the standard timers to stock and maintain an inventory. An overview of the system is shown in Figure 1.
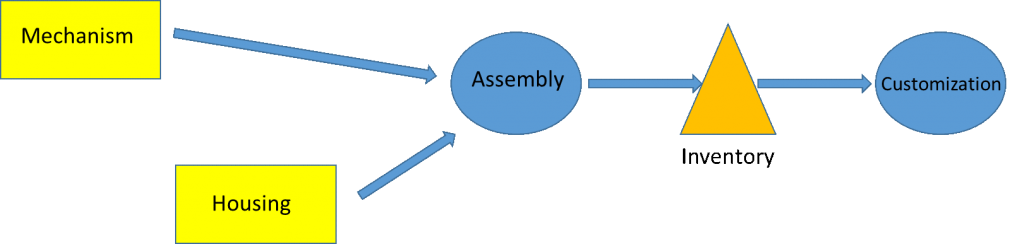
One might manage and plan this system in a variety of ways; but the most common way is to assume that we can associate a planned lead time with each activity, as I describe next.
How do we manage and size the inventory of timers? We need to know how long it takes to replenish the inventory, which is the time to get the mechanism plus the time for assembly [1]. Typically we have some understanding with the machine shop as to how long it takes to complete an order for the mechanism; and we have some expectation of how long it takes to accomplish the assembly once we have the components. For instance, we might plan on ten weeks for the completion and delivery of the mechanisms, and then allow for two weeks for the assembly. Then we would size our inventory based on the planned lead time of twelve weeks to replenish the inventory.
How do we plan inventory replenishment? If the planned lead time is twelve weeks, then we would initiate a replenishment when our inventory position [2] is not sufficient to cover our demand forecast over the planned lead time, namely the next twelve weeks, based on some desired service level. This would trigger the replenishment of mechanisms. We also rely on planned lead times for ordering the housings. Obviously we cannot do the assembly without both components. If we expect (say) a four-week lead time for the housing from our plastic injection operation, then we time the order to arrive concurrent with the mechanisms so as to not delay assembly.
How do we set a customer promise? Finally, we use planned lead times to quote a service time to customers. If we plan for one week to complete the customization process, then we promise our customers a one-week turnaround on any order [3].
We appreciate that the actual lead times may exhibit uncertainty. For instance, sometimes the machine shop may need more or less time to fill an order. Possibly we can model the actual lead times with a probability distribution. And in theory, one might plan and manage this system by explicitly accounting for these uncertainties. But this is seldom done in practice, as it’s too complex, even in a system as simple as the example. Rather, we will pad the planned lead time to cover the uncertainty.
Furthermore, in a supply chain, it is common practice for different parties to do business based on a deterministic lead time. A manufacturer’s contract with a supplier will specify a delivery lead time, which serves as the planned lead time for the manufacturer’s planning. And this delivery lead time is set as a constant, not as a random variable with some probability distribution. Similarly, in our example, the customer wants to know when they can pick up their customized timer, and will not accept a probabilistic commitment.
Why are planned lead times important?
As noted above, planned lead times are critical parameters in planning systems, and are essential to the creation of production, procurement and material release plans. But beyond this, planned lead times effectively determine a firm’s work-in-process (WIP) level. If I have a production stage with a planned lead time of three weeks, then I release work to the stage three weeks before it is due, even though the actual work content might be a few days or even hours. I then manage the production activity so that the flow time (which is largely wait time) matches the planned lead time of three weeks; as a consequence, I will have on average three weeks of WIP inventory. This is basically an application of Little’s Law.
Hence setting the planned lead times is an investment decision. It determines the amount of inventory in process.
Furthermore, planned lead times are important because they are often self-fulfilling prophecies: if we plan an activity to take, say, three weeks, then we will load the activity with work three weeks before it is due and, not surprisingly, it will take three weeks (or more, if something goes wrong) before the work passes through the activity. This can also result in a vicious cycle: We start with a three-week planned lead time and load the activity up with three weeks of WIP. Something goes wrong and we lose some capacity, and some of the work takes longer than three weeks. So we increase the planned lead time to four weeks, and now release work four weeks before it is due, and hence increase the WIP and the actual lead time increases too….
What are the trade-offs to consider in setting planned lead times?
The setting of a planned lead time for a production resource or process stage equates to setting a buffer (in the form of WIP) to accommodate any mismatch between the variable workload requirements on a resource and the resource’s capability. This buffer smooths the variable workload requirements on a resource; the larger is the buffer, the more damping (or smoothing) that it can do. The size of the buffer, and hence the length of the planned lead time, depends on how much smoothing is needed to bring the variable workload in accord with the process capabilities of the resource.
The key determinants for the planned lead time for a resource or stage are: the variability in the workload requirements, the flexibility of the resource to adjust its rate of production, and the amount of headroom in the system. In the appendix we develop a simple model for the relationship between the planned lead time and these factors; here we will illustrate these relationships with an example.
Consider the assembly process from the above example, and suppose that it is a shared resource that does assembly for a large family of timing devices, including the kitchen timer. We suppose that the time period for planning is a work day.
We express the workload requirements on the assembly process in terms of units of capacity, and for this example, let’s suppose capacity is measured in hours per day of assembly time. From past history we project that the demand (or workload) on the assembly process is µ hours per day with a standard deviation of σ hours per day. We denote the capacity (or capability) of the assembly process to be µ + χ hours per day, where we interpret this to be the maximum reasonable output level for this resource. We expect that the capability exceeds the demand; that is, χ > 0 which denotes the headroom (or extra capacity) that is available for handling variability in the workload.
With a simple model [4] (see appendix), we can relate these system parameters to prescribe the planned lead time n for this process:
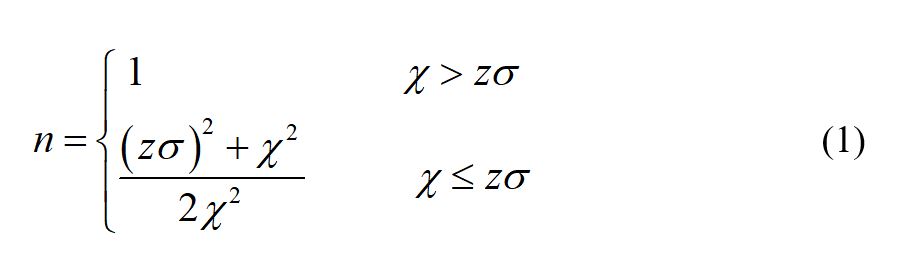
where z is a service factor, related to how frequently the required production might exceed the capacity. For instance, under an assumption that the variability in the system follows a normal distribution, then a service factor z = 1.64 (or z = 2.05) would correspond to a service level on the capacity of 95% (98%); that is, we expect that on one day in 20 (one day in 50), we would need for the assembly process to do more work than its nominal capacity of µ + χ hours. This might happen through overtime, or by working faster, or by diverting more resources to the process than normal.
We see from (1) that the planned lead time is one time period (one day) when the headroom exceeds the workload variability; that is, when we have enough slack to handle any daily variability, then we need no buffer. When the headroom is less than the workload variability, then we need a buffer and the planned lead time increases exponentially with less headroom, as shown in the following figure for σ = 20 hours per day, z = 2.05:
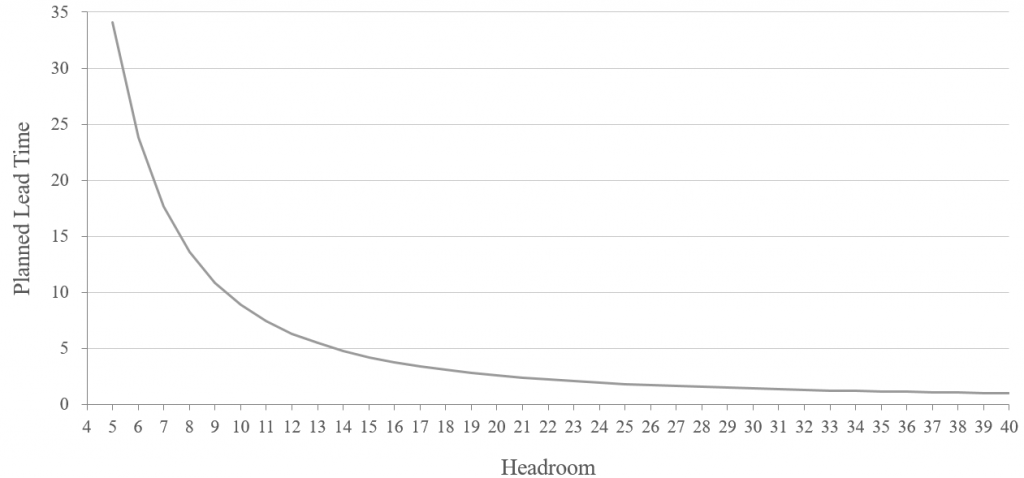
Thus, we have a tradeoff between the headroom, or excess capacity, and the planned lead time, which maps directly into the work-in-process level.
Similarly we might look at how the planned lead time increases as the workload variability increases, for a fixed amount of headroom ( χ = 10 hours per day, z = 2.05):
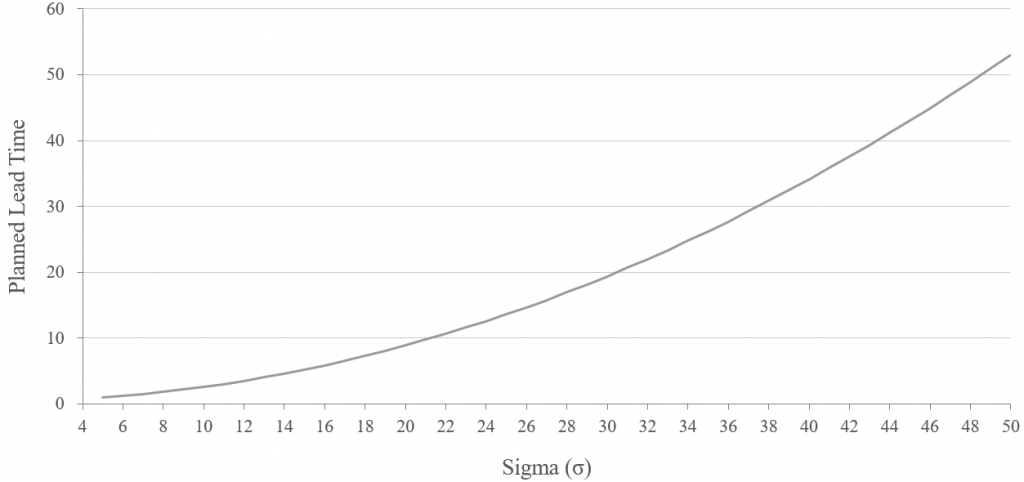
As expected the more variability in the workload, the greater the planned lead time, as we need a larger buffer to smooth this variability. Again, we have a tradeoff.
A lower service level will reduce the planned lead time; this would then lead to more frequent “service violations,” in terms of days when the production requirements will exceed the nominal resource capacity, and hence require some exceptional actions (like overtime). Thus, there’s another tradeoff here to consider.
Thus, from this simple model (1), we have three levers to affect the planned lead time: we can increase the headroom, or decrease the workload variability, or reduce our service level. Each has a cost, and what one does will (as always) depend on the context.
Summary
In this note, we have tried to convey:
- Planned lead times are critical control parameters in most planning systems, and have not been extensively studied or modeled.
- Planned lead times are commonly set experientially, and often in reaction to extreme events
- Planned lead times are investment decisions in that they determine the WIP inventory
- Planned lead times are self-fulfilling prophecies
- The setting of a planned lead time should depend on the variability of the workload, the amount of resource headroom, and the flexibility of the resource to vary its output rate.
For sure, future planning systems may become more sophisticated, may be more data driven and computationally intensive. As such these planning systems may be more intelligent, and less dependent on planned lead times. But until we get there, there are opportunities to improve how we set, manage and think about these planning parameters.
Notes
[1] We will assume that we do not keep an inventory of components.
[2] Inventory on hand plus inventory in process or on order.
[3] Under the assumption that we have inventory on hand.
[4] As shown in the appendix, this formula is from a simple model built from a series of assumptions. We don’t purport that this model would apply universally, let alone that it is the only way to look at how to determine planned lead times. Rather it is one way with the intent of highlighting how the key factors interact, with the intent of providing some insight and guidance on how to set and affect the planned lead time.
